首先介紹幾個概念

①改進的booth編碼：

       booth編碼用于乘法計算中對乘數進行重新編碼，目的是減少加法的次數，減少程序的運行時間。本設計中，考慮8*8的乘法，對于一個8位的乘數，采用基四編碼的思想編碼，最終產生4個部分積相加（若不編碼則會產生8個部分積），具體的編碼規則如下：

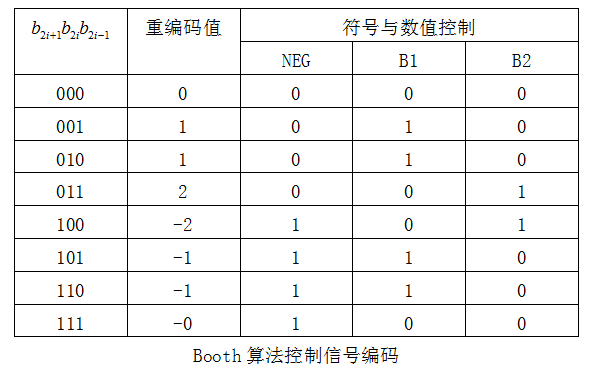
       簡單點來說，當考慮算法時，上表中僅有重編碼值對我們有研究意義，將8位被乘數最后補一個零，將9位被乘數b₇b₆b₅b₄b₃b₂b₁b₀0分為四組編碼進行編碼：b₇b₆b₅、b₅b₄b₃、b₃b₂b₁、b₁b₀0。每一組對應一個重編碼值，如不考慮重編碼值對于部分積的影響，四個部分積（均為十六位）應該表示為：xxxxxxxxa、xxxxxxa00、xxxxa0000、xxa000000，其中a為8位被乘數，x為擴展位，x值和a的最高位相同，低位均補零。當考慮重編碼值對部分積的影響時，部分積發生變化如下（僅僅用十六位中的a來說明就可以，因為a確定了十六位數就確定了）：

當重編碼值為0時，部分積為0；

當重編碼值為1時，a不變；

當重編碼值為-1時，a變為-a(取反加1)；

當重編碼值為2時，a左移一位；

當重編碼值為-2時，a左移一位后將a變為-a（取反加1）；

②Wallace樹部分積壓縮算法：

假設用booth編碼后的十六位部分積用P1、P2、P3、P4表示，壓縮算法可以減少版圖的關鍵路徑和所需加法器的單元數目，具體的壓縮算法方法如下圖所示：（由于符號位可能為1也可能為0，所以高位不確定，但補位時低位一定為零，把可能為非零的數用*表示）

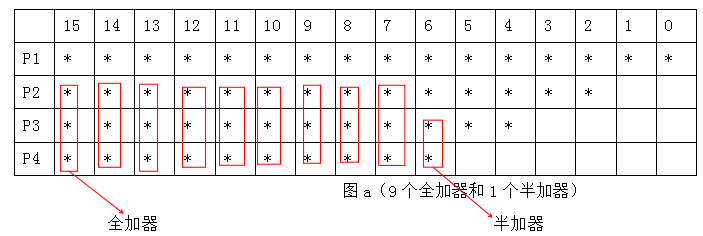
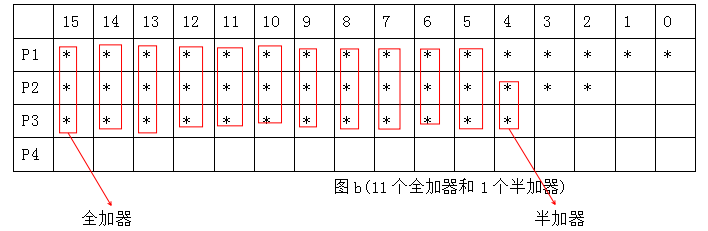
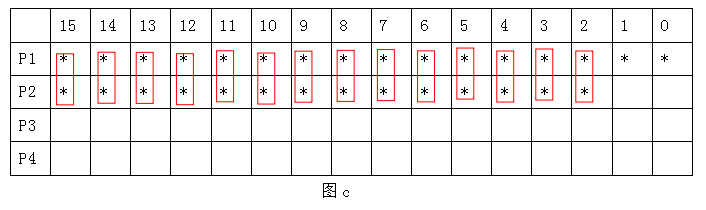
 經過圖a和圖b的兩次Wallace數部分積壓縮，最后的數據呈現圖c上，一共需要20個全加器和2個半加器，最后僅需將p1和p2由一個簡單的兩輸入加法器完成加法即可。（注：最后也可以將p1[2]和p2[2]由一個半加器相加，第三位到第十五位由全加器相加，由此完成加法效果相同，此方法的程序也在后面的程序中給出）

 需要注意，無論是半加器還是全加器，和保存在本位，進位保存在下一位。舉例說明如下：考慮圖b中的p1[5],p2[5],p3[5]相加，其和保存在p1[5],進位保存在p2[6]。圖a和圖b均為從高位向低位運算。

 本設計中包含兩個功能模塊：booth編碼模塊和Wallace數壓縮算法模塊。booth編碼模塊根據被乘數或者乘數改變為運行開始的信號，Wallace數壓縮算法根據外加的一個時鐘信號的上升沿為運行開始的信號。

 驗證系統功能時用以下三組數據驗證：

          10100111*01101101

          11111011*11111011

          00001010*00000011

     結果如下所示：

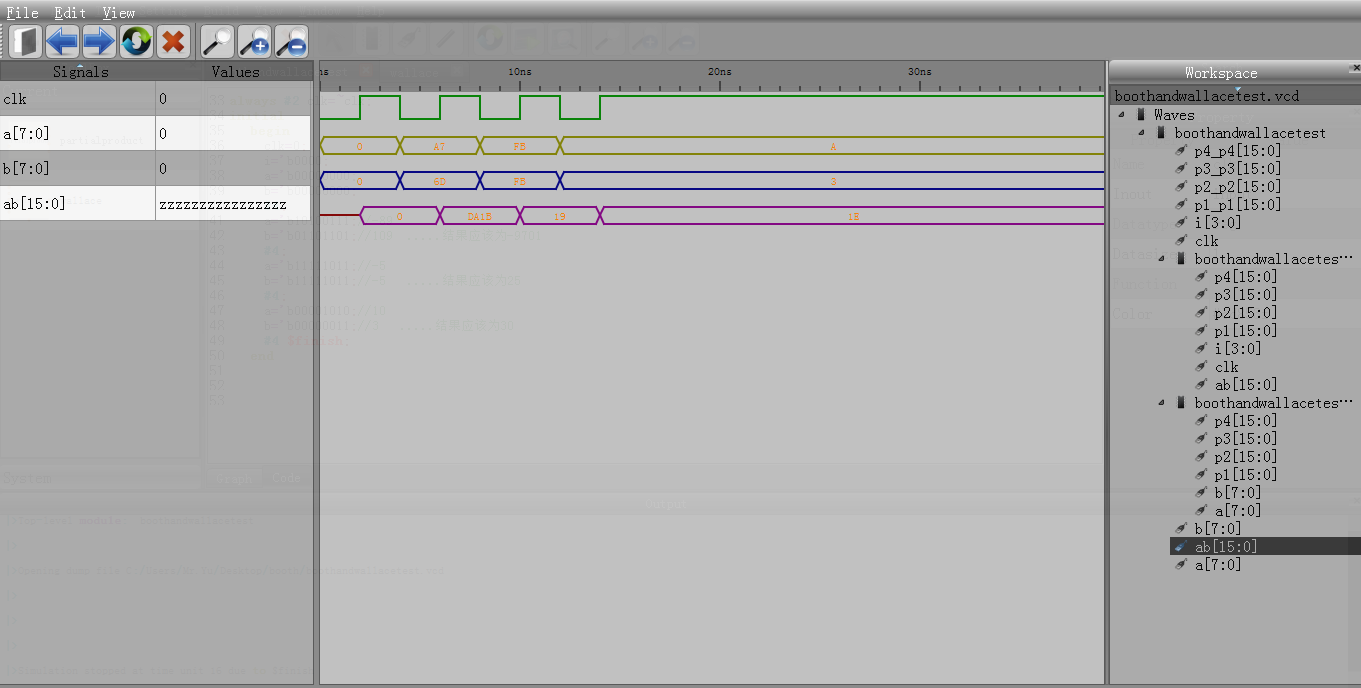    結果顯示：10100111*01101101=DA1B即（-89）*109=-9701

              11111011*11111011=19即（-5）*（-5）=25

              00001010*00000011=1E即10*3=30

    部分積經驗證全部正確；

    測試數據涵蓋了所有的情況（負乘以正，負乘以負，正乘以正），結果均符合實際情況。

    需要注意：運算中涉及到負數用補碼表示；